Geometric shapes-inspired designs. From bold triangles to sophisticated hexagons, each sheet is a masterpiece waiting to enhance your presents, be it Christmas, birthdays or beyond.

Unleash the avant-garde allure of our geometric wrapping paper collection. Each design is a mathematical masterpiece, tailored to transform your gifts into bold statements of individuality.

Wrap with distinction and elevate your gifting game to the next level.

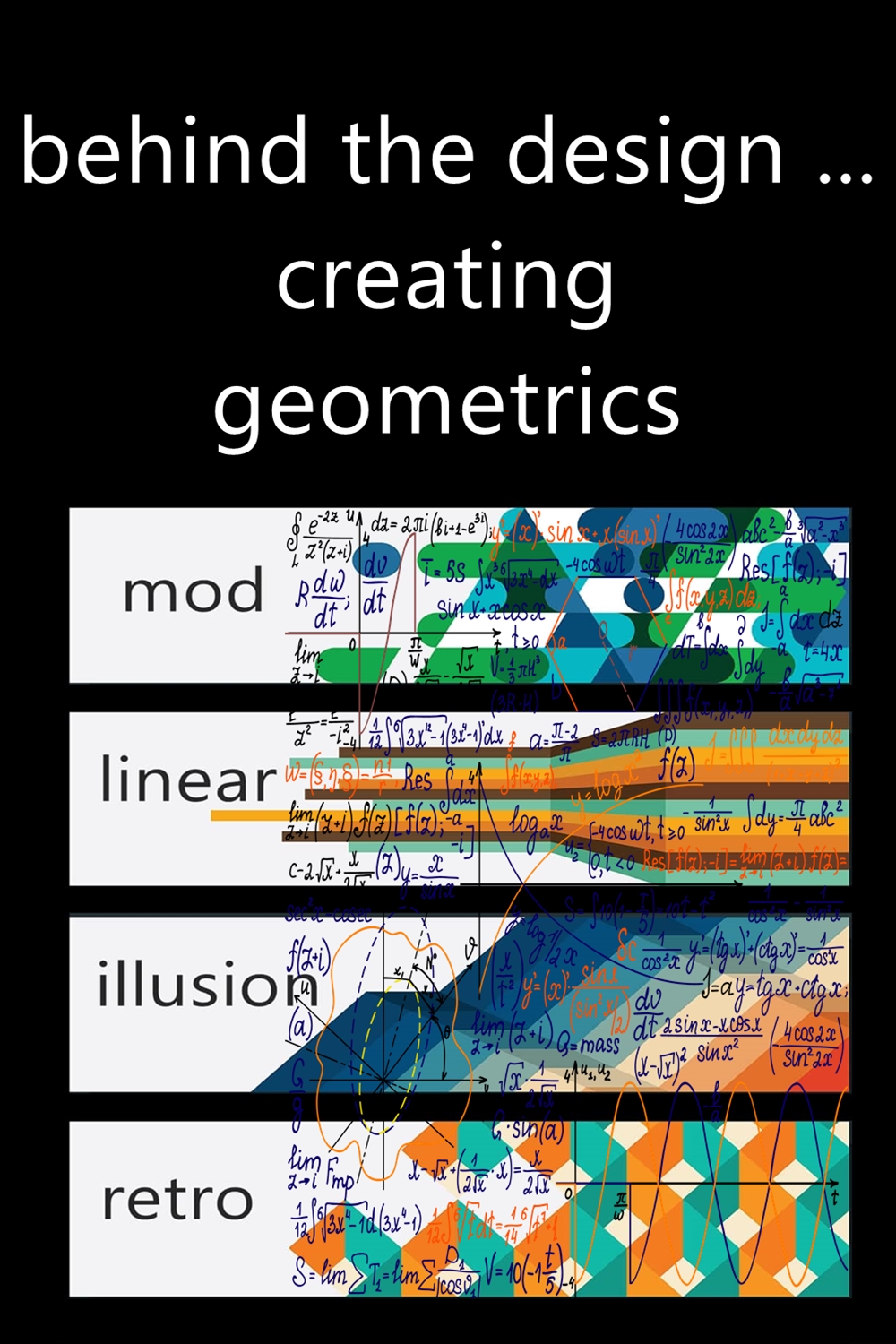
Here’s a simplified breakdown of the math behind creating geometric designs:

1. Symmetry and Repetition: Geometric patterns often rely on symmetry and repetition to create visually appealing designs. Mathematical concepts such as tessellation, where shapes fit together without any gaps or overlaps, are frequently used.
2. Basic Shapes and Angles: Many geometric designs start with basic shapes such as squares, triangles, circles, or hexagons. Understanding the properties of these shapes, including their angles and proportions, helps in creating balanced and harmonious patterns.
3. Grids and Proportions: Grids are commonly used as a framework for creating geometric designs. By dividing the wrapping paper into equal sections or using a predefined grid system, designers can ensure consistency and precision in their patterns.
4. Color Theory: While not strictly mathematical, color theory plays a crucial role in geometric design. Understanding concepts such as complementary colors, contrast, and color harmonies helps in selecting colors that enhance the visual impact of the geometric pattern.
5. Software Tools: Designers often use graphic design software such as Adobe Illustrator or geometric design generators to create and manipulate geometric patterns. These tools allow for precise measurements, transformations, and repetitions, streamlining the design process.
6. Complexity and Iteration: As geometric patterns become more intricate, the math involved becomes more complex. Designers may use algorithms or mathematical formulas to generate complex patterns or iterate on designs to achieve desired results.

Creating a circle involves understanding its key elements:

1. Radius: The distance from the center to any point on the circle’s edge.
2. Diameter: Twice the length of the radius, it’s the distance across the circle through its center.
3. Circumference: The total length around the circle, calculated as π times the diameter or 2π times the radius.
4. Area: The space enclosed by the circle’s boundary, calculated as π times the square of the radius.

These mathematical principles enable precise construction and measurement of circles in various applications, from geometry to engineering and beyond.

🎨

Creating a triangle involves understanding its fundamental properties:

1. Sides: A triangle has three sides, each connecting two vertices (corners).
2. Angles: Three angles exist within a triangle, with their sum always totaling 180 degrees.
3. Types: Triangles can be classified based on their side lengths (equilateral, isosceles, or scalene) or angles (acute, obtuse, or right).
4. Area: The area of a triangle can be calculated using the formula A = 1/2 * base * height, where the base is any one side, and the height is the perpendicular distance from the base to the opposite vertex.

Understanding these mathematical principles allows for precise construction and measurement of triangles, which are foundational shapes used in various fields such as geometry, engineering, and architecture.

Creating a square involves understanding its core attributes:

1. Sides: A square has four equal sides, forming four right angles at each corner.
2. Diagonals: Two diagonals connect opposite corners of a square, bisecting each other at right angles and having the same length as the side of the square multiplied by the square root of 2.
3. Area: The area of a square can be calculated using the formula A = side * side, where “side” represents the length of one of its sides.
4. Perimeter: The perimeter of a square is the total length of its four sides, calculated as P = 4 * side.

Understanding these fundamental properties enables precise construction and measurement of squares, which are ubiquitous geometric shapes used in various applications, from architecture and engineering to mathematics and art.

🎨

Understanding the fundamentals of a rectangle involves:

1. Sides: A rectangle has two pairs of parallel sides, with opposite sides having equal lengths.
2. Angles: All four angles of a rectangle are right angles, measuring 90 degrees.
3. Diagonals: The diagonals of a rectangle are equal in length and bisect each other, creating congruent right triangles.
4. Area: The area of a rectangle can be calculated using the formula A = length * width, where “length” represents the longer side and “width” represents the shorter side.
5. Perimeter: The perimeter of a rectangle is the sum of all its sides, calculated as P = 2 * (length + width).

Understanding these principles enables precise construction and measurement of rectangles, which are common shapes found in architecture, engineering, and everyday objects.

Grasping the fundamentals of geometric shapes relevant to wrapping paper design involves:

1. Circles: Circles add fluidity and movement to patterns, creating dynamic and visually pleasing designs. Their curves contrast with straight lines, adding balance and interest to the overall composition.
2. Triangles: Triangles bring structure and energy to patterns, offering sharp angles and geometric precision. They can be arranged in various orientations and sizes to create bold and dynamic arrangements.
3. Squares and Rectangles: Squares and rectangles provide stability and symmetry to patterns, serving as foundational elements that anchor the design. Their uniform shapes create a sense of order and cohesion, making them versatile building blocks for geometric patterns.
4. Hexagons: Hexagons introduce complexity and intricacy to patterns, offering a unique blend of symmetry and asymmetry. Their six sides and angles allow for endless arrangement possibilities, adding depth and dimension to the design.
5. Diamonds and Rhombuses: Diamonds and rhombuses add sophistication and elegance to patterns, offering a sense of refinement and luxury. Their angular shapes create visual interest and can be rotated or repeated to create captivating motifs.

Final Thoughts

In conclusion, the use of mathematics in the creation of geometric wrapping paper is essential for achieving precision, symmetry and visual appeal. From determining the dimensions of the paper to calculating the angles and measurements of intricate geometric patterns, mathematics plays a crucial role in every aspect of Paint2Pixels design process. By understanding the mathematical principles behind geometric shapes and patterns, designers can create visually stunning and unique wrapping paper that adds an extra touch of sophistication to any gift. So next time you’re wrapping a present, remember that behind the beautiful design lies the power of mathematics.